Simultaneidad de eventos y relatividad
Como ya vimos, 1905 fue el annus mirabilis de Albert Einstein. Ese año publicó el primer artículo con la teoría de la relatividad (Einstein, 1905). Concretamente habló de la relatividad especial y del comportamiento relativista de la materia, mostrando efectos sobre la longitud y el tiempo. Por otro lado, también habló de la relación entre materia y energía. En esta serie de dos textos, o tres, según vea, hablaremos de la percepción en base a la física clásica y la física relativista, como la simultaneidad de eventos, la contracción de las longitudes o la dilatación del tiempo. También mostraremos un caso real de comportamiento relativista como es el del muon, una partícula subatómica de lo más interesante.
En este primer texto hablaremos de la simultaneidad de eventos, aunque antes de nada, conviene establecer los pilares de la relatividad especial y es por eso que debemos comprender los dos principios fundamentales, que se describirán a continuación. Por otro lado, en este texto habrá ecuaciones, aunque quien quiera ver los fenómenos descritos cualitativamente, podrá hacerlo sin prestar atención a ellas, tan solo a la descripción y las conclusiones. Por supuesto, quien quiera analizarlas, comprenderá los fenómenos a nivel cuantitativo.
Los principios fundamentales de la relatividad especial
Albert Einstein fue un físico puramente teórico y apenas pisó un laboratorio por lo que todas sus conclusiones estaban basadas en cálculos y no en resultados empíricos. El tiempo ha ido dándole la razón en numerosas ocasiones, incluso en tiempos actuales. Para teorizar sobre su relatividad especial en su artículo «Sobre la electrodinámica de los cuerpos en movimiento» (ver Referencias), estableció dos principios que, a priori pueden parecen contradictorios pero que si hablamos de marcos relativistas, se complementan a la perfección. Estos principios son los siguientes:
Principio de relatividad
El principio de la relatividad establece que las leyes de la física son las mismas para todos los observadores en movimiento uniforme, por lo que descarta los marcos de referencia absolutos. Es decir, un observador que está dentro de un vehículo completamente opaco, no podrá determinar si está en reposo o si está viajando a una velocidad constante.
Una conclusión de este principio de relatividad es que no hay un movimiento absoluto. Es decir, el movimiento siempre tiene que ser relativo a un marco de referencia. Otra conclusión está en la invarianza de las leyes físicas, lo que quiere decir que todos los observadores, independientemente de cómo se estén moviendo, estarán sujetos a las mismas leyes físicas.
Principio de la constancia de la velocidad de la luz
El principio de la constancia de la velocidad de la luz nos dice que, en el vacío, cualquier observador medirá la velocidad de la luz como su valor «c», o lo que es lo mismo, 299.792 km/s, independientemente del sentido, velocidad o posición del observador. Es decir, si dos observadores van uno hacia el otro a una velocidad cualquiera y uno de ellos dispara un rayo de luz, el que dispara verá que la luz se desplaza a una velocidad «c», pero el que va a recibir el rayo, también la verá desplazarse a una velocidad «c».
La consecuencia más radical de esto es que dos eventos que son simultáneos para un observador «A», pueden no serlo para un observador «B». Otra consecuencia es que si un observador «A» observa moverse a un observador «B», si el observador «A» pudiese ver el reloj de «B», vería que el reloj de «B» se desplaza más lentamente que el suyo. Sin embargo, «B» observará que su reloj funciona correctamente.
Simultaneidad de eventos: bolas de paintball y láseres
Para ver un ejemplo de dos comportamientos aparentemente similares, vamos a recrear dos experimentos. El primero de ellos será mediante un experimento con bolas de paintball en un vagón que inicialmente estará detenido y luego viajará a velocidad constante. El segundo experimento será similar al anterior pero en lugar de disparar bolas de paintball, se dispararán dos luces láser. En ambas situaciones, descartaremos tanto la fuerza de la gravedad como el rozamiento por el aire para trabajar con unas condiciones lo más simplificadas posible.
1) Las bolas de paintball
Planteemos las condiciones iniciales:
- Tenemos un vagón de longitud «L».
- Hay dos detectores situados en los extremos del vagón separados una distancia «L».
- Tenemos un dispositivo fijo a pie de vía que lanza bolas de paintball hacia la derecha y hacia la izquierda a la misma velocidad (Vp) para impactar en los detectores.
¿Cómo se activa el lanzador de pelotas? Puede activarse manualmente cuando el vagón está parado. Si está en movimiento con una velocidad V constante, en el centro justo del vagón hay un sensor que cuando pasa por delante del dispositivo, dispara automáticamente dos pelotas, una hacia cada lado. Además, cuando una pelota impacta en un detector, el detector se ilumina de color verde.
Por otro lado, tenemos dos métodos de observar el experimento a los que llamaremos «Observador A» o, simplemente A y «Observador B» o simplemente B. Ambos observadores pueden determinar con precisión la velocidad de cada una de las bolas, la distancia que recorre cada una de ellas y el tiempo que la bola tarda en hacer el recorrido, con la siguiente particularidad:
- El «Observador A» está situado dentro del vagón, justo en su punto medio.
- El «Observador B» está situado fuera del vagón, justo detrás del dispositivo que lanza las pelotas.
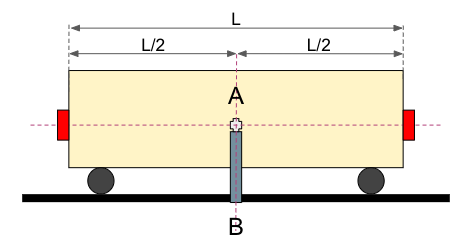
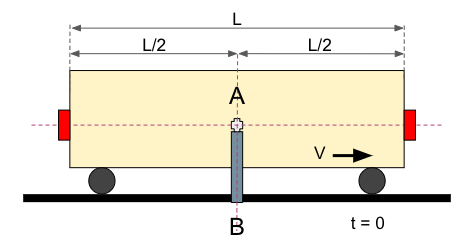
Este sería el esquema del vagón que vamos a utilizar:
Experimento 1.1: el vagón está parado
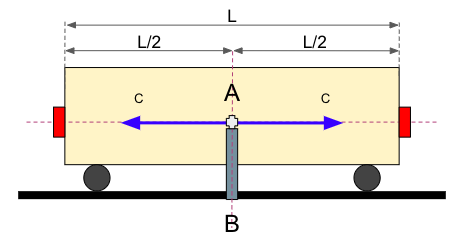
En este primer experimento, la velocidad del vagón es V = 0. Entonces, en t = 0 se lanzan las bolas por lo que a mitad de vuelo tenemos este escenario:
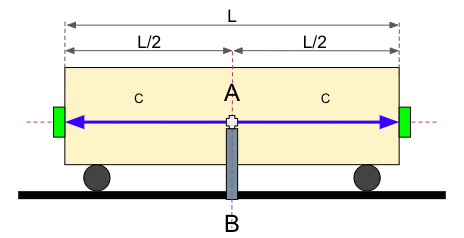
Finalmente, las bolas llegan a sus detectores correspondientes. La bola que viaja hacia la derecha llega al detector en t = tdcha mientras que la bola que viaja hacia la izquierda llega al detector en t = tizqd. Este sería el escenario:
Al llegar las bolas a los detectores, ambos observadores miden el mismo tiempo empleado por lo que el evento de choque ha sido simultáneo. ¿Qué valores tendrán los tiempos tdcha y tizqd? Serían los siguientes:
Conclusión: hay simultaneidad de eventos
Podemos ver que tdcha y tizqd son iguales y, por lo que, efectivamente, las dos bolas impactan a la vez en los detectores, tanto para A como para B por lo que existe simultaneidad de eventos
Experimento 1.2: el vagón está en movimiento
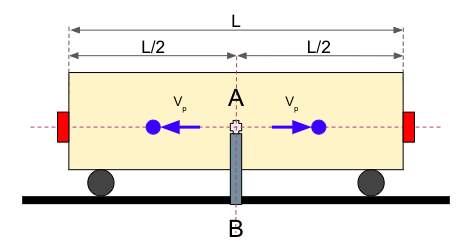
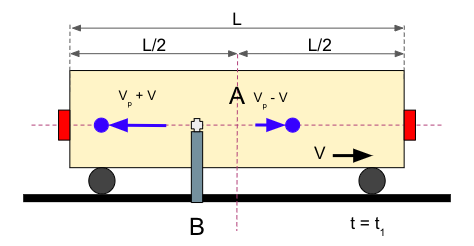
Este experimento es similar al anterior solo que con el vagón en movimiento. El vagón se desplaza a una velocidad constante V mayor que 0 hacia la derecha, aunque menor que la velocidad de disparo VP. A efectos prácticos, nos da igual la velocidad que sea, siempre y cuando sea constante. En el momento t = 0, que es cuando la parte central del vagón pasa frente al dispositivo, se lanzan dos pelotas. ¿Qué aprecia cada observador? Estas serían las condiciones iniciales:
Lo que observa A
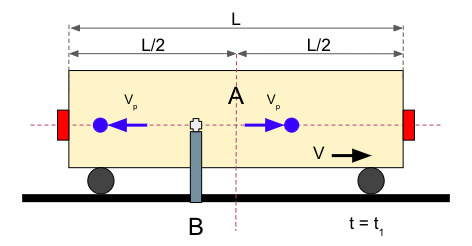
El Observador A desde su marco de referencia observa que cada bola recorre el mismo recorrido, es decir L/2. Sin embargo, como A está en movimiento, la velocidad que aprecia en las bolas es diferente: La velocidad de la bola que viaja en el sentido del vagón es Vp – V, menor que la velocidad que viaja en sentido contrario, que es Vp + V. La situación que vería A con las dos bolas en vuelo sería esta:
En este caso, el Observador A aprecia como la bola que viaja hacia la izquierda impacta antes en el detector, iluminándose en verde:
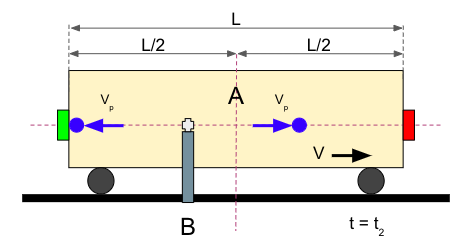
Para el Observador A, el tiempo que ha estado en vuelo la bola que viaja hacia la izquierda tiene un valor que obedece a esta expresión:
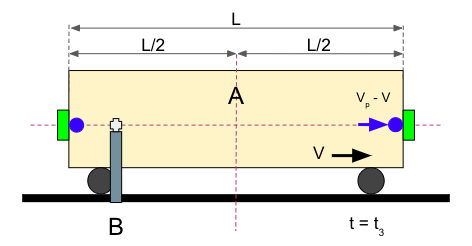
Por último, la bola que viaja hacia la derecha impacta en el detector:
Para el Observador A, el tiempo que ha estado en vuelo la bola que viaja hacia la derecha tiene un valor que obedece a esta expresión:
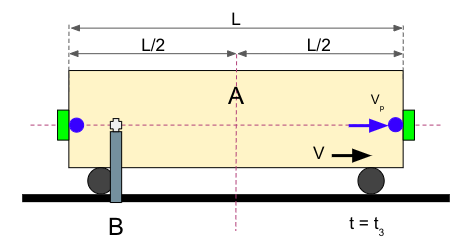
Lo que observa B
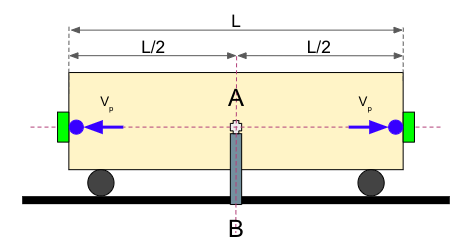
El Observador B desde su marco de referencia viendo todo desde fuera del vagón observa que ambas bolas viajan a la misma velocidad, es decir, a Vp. Sin embargo, las distancias que recorren las bolas son distintas. La distancia de la bola que viaja en sentido contrario del vagón es (L/2 – x), que es menor que la que recorre la bola que viaja en el mismo sentido del vagón, que es (L/2 + y). La situación que vería B con las dos bolas en vuelo sería esta:
El Observador B también aprecia como la bola que viaja hacia la izquierda impacta antes en el detector, iluminándose en verde:
Para el Observador B, el tiempo que ha estado en vuelo la bola que viaja hacia la izquierda tiene un valor que obedece a esta expresión:
Finalmente, la bola que viaja hacia la derecha impacta en el detector:
Para el Observador A, el tiempo que ha estado en vuelo la bola que viaja hacia la derecha tiene un valor que obedece a esta expresión:
Conclusión: hay simultaneidad de eventos
A pesar de que las expresiones que obtienen los observadores A y B son diferentes, los tiempos que han medido para la bola que viaja hacia la izquierda, coinciden. Del mismo modo, también coinciden los tiempos de la bola que viaja a la derecha por lo que podemos asegurar que hay simultaneidad de eventos. Ahora daremos un paso más, que es igualar ambas expresiones para de este modo, calcular los valores de x e y:
Ahora, si sustituimos x e y en las diferentes expresiones del Observador B para ambas bolas, lo que obtenemos es una expresión general que nos ofrece el tiempo empleado por cada bola ante cualquier situación:
Analizando estas ecuaciones podemos obtener datos realmente interesantes:
- Si V = 0. Por ejemplo, si suponemos que el vagón está en reposo (V = 0), al sustituir para cada bola en las expresiones de arriba obtenemos el mismo resultado que obtuvimos cuando supusimos que el vagón estaba en reposo.
- Si V = Vp. Si suponemos que el vagón viaja a la misma velocidad que la velocidad de disparo (V = Vp), tendríamos que la bola que se desplaza hacia la derecha tendría un denominador cero, lo que implica un tiempo infinito, algo coherente porque la bola nunca tocaría la pared derecha.
2) Las luces láser
En este segundo planteamiento, en lugar de usar bolas de paintball lo que nuestro dispositivo va a hacer es encender dos luces láser: una se desplazará hacia la derecha y otra hacia la izquierda. Haremos dos experimentos: uno con el vagón parado y otro con el vagón en movimiento a una velocidad constante y veremos lo que aprecian los observadores A y B. En este caso, los observadores también pueden saber la distancia que recorre cada rayo de luz así como el tiempo que tardan en impactar. La velocidad de los rayos, será la velocidad de la luz o «c»
Experimento 2.1: el vagón está parado
En este primer experimento, la velocidad del vagón es V = 0. Entonces, en t = 0 se encienden las luces láser y en un momento determinado tenemos este escenario:
Finalmente, los rayos de luz láser llegan a sus detectores correspondientes. La luz que viaja hacia la derecha llega al detector en t = tdcha mientras que la luz que viaja hacia la izquierda llega al detector en t = tizqd. Este sería el escenario:
Al llegar las luces a los detectores, ambos observadores miden el mismo tiempo empleado por lo que el evento de choque ha sido simultáneo. ¿Qué valores tendrán los tiempos tdcha y tizqd? Serían los siguientes:
Conclusión: hay simultaneidad de eventos
Podemos ver que tdcha y tizqd son iguales y, por lo que, efectivamente, los dos rayos láser impactan a la vez en los detectores, tanto para A como para B por lo que sí que tenemos simultaneidad de eventos.
Experimento 2.2: el vagón está en movimiento
Este experimento es similar al anterior solo que con el vagón en movimiento. El vagón se desplaza a una velocidad constante V mayor que 0 hacia la derecha. En el momento t = 0, que es cuando la parte central del vagón pasa frente al dispositivo, se lanzan los dos rayos de luz láser. ¿Qué aprecia cada observador?
Lo que observa A
El Observador A desde su marco de referencia observa que cada rayo de luz láser recorre el mismo recorrido, es decir L/2. Sin embargo, en base al principio de la constancia de la velocidad de la luz, la luz viaja a la misma velocidad en ambas direcciones por lo que impactarán a la vez en los detectores. Es decir, el observador A no aprecia el rayo que va en sentido opuesto al vagón con una velocidad c + v y el que va a favor con una velocidad c – v.
Einstein, en su principio de constancia de la velocidad de la luz estableció que la máxima velocidad alcanzable en el universo era c, la velocidad de la luz. Por lo tanto, el observador A no podría apreciar una velocidad c + v, sino c. Por lo tanto, por coherencia, el rayo que viaja en sentido contrario no experimentaría una velocidad c – v, sino c también. Bajo esta premisa, el Observador A tendrá un resultado similar al caso anterior en cuanto a los tiempos en los que la luz ha estado viajando:
Lo que observa B
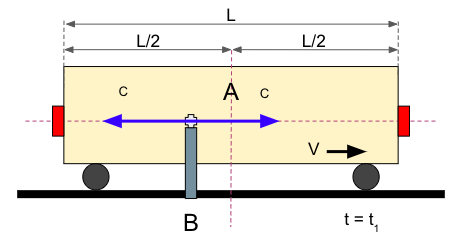
El Observador B desde su marco de referencia, viendo todo desde fuera del vagón, observa que ambos rayos de luz viajan a la misma velocidad debido al principio de la constancia de la velocidad de la luz. Sin embargo, las distancias que recorren los rayos de luz son distintas. La distancia de la luz que viaja en sentido contrario del vagón es (L/2 – x), que es menor que la que recorre la luz que viaja en el mismo sentido del vagón, que es (L/2 + y). La situación que vería B con los dos rayos de luz en vuelo sería esta:
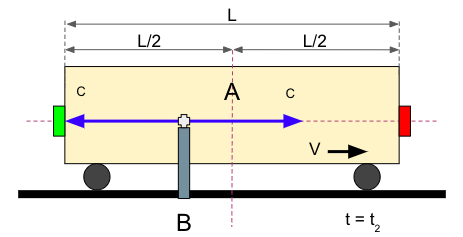
El Observador B, a diferencia del Observador A, aprecia como la luz que viaja hacia la izquierda impacta antes en el detector, iluminándose en verde:
Para el Observador B, el tiempo que ha estado en vuelo la bola que viaja hacia la izquierda tiene un valor que obedece a esta expresión:
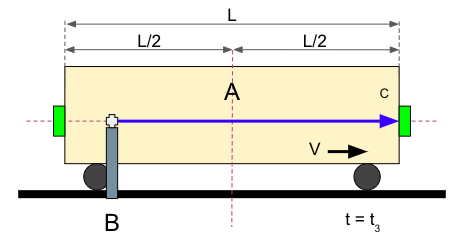
Finalmente, la luz que viaja hacia la derecha impacta en el detector:
Para el Observador B, el tiempo que ha estado en vuelo la luz que viaja hacia la derecha tiene un valor que obedece a esta expresión:
Conclusión: NO hay simultaneidad de eventos
En esta ocasión, ante un mismo evento, A y B comprueban que sus resultados de medir el tiempo han sido diferentes tanto para la luz que se desplazaba hacia la izquierda como para la que se desplazaba hacia la derecha. En este caso, no tenemos simultaneidad de eventos para los observadores A y B por el hecho de que las bolas no están sujetas al principio de la constancia de la velocidad de la luz pero los rayos de luz sí que lo están.
De este modo podemos comprobar con dos experimentos teóricos muy sencillos, como los resultados pueden escapar a nuestros sentido común. Hemos visto que en un caso los resultados con coherentes con nuestra percepción pero en el otro caso, el resultado rompe con nuestro sentido común por el hecho de percibir un mismo evento. Para eso está la teoría de la relatividad especial: analizar, entre otras cosas, si un mismo evento resulta simultáneo para dos observadores. A esto se le conoce como «relatividad de la simultaneidad».
Referencias
Einstein, A. (1905). Zur Elektrodynamik bewegter Körper. Annalen der Physik, 322, iss. 10. DOI: 10.1002/andp.19053221004 (Ver).
- Antonio Pérez Verde
- 30/03/2024
- 3 Comment

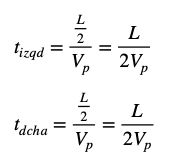

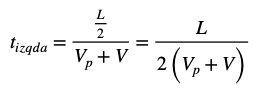
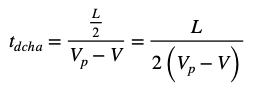
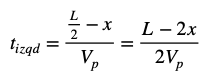
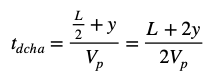
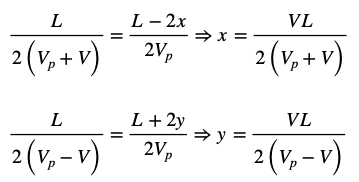
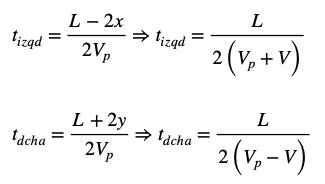
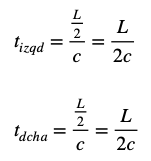
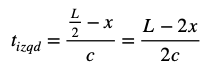
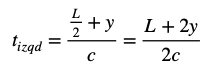











3 Comentarios