El problema de los tres cuerpos

Hablemos de Física… El motivo es que se está hablando mucho de «El problema de los tres cuerpos» porque el próximo 21 de marzo se va a estrenar una serie con ese nombre en una plataforma de streaming. Según la sinopsis de este servicio, trata de cinco eruditos que hacen peligrosos descubrimientos a través del tiempo y el espacio. La consecuencia es que a medida que van desvelando las leyes de la ciencia, surge una amenaza para la humanidad.

La serie está basada en tres novelas escritas por Cixin Liu (1963-…) conformando la trilogía El recuerdo del pasado de la Tierra, publicada entre 2006 y 2010. Están considerados dentro del género Hard SciFi y está compuesta por los títulos:

• El problema de los tres cuerpos (2006).
• El bosque oscuro (2008).
• El fin de la muerte (2010).

Quienes decidan ver la serie (yo entre ellos), está protagonizada por Jess Hong, Liam Cunningham y Eiza González, y sus creadores son David Benioff (Juego de Tronos), D.B. Weiss (Juego de Tronos) y Alexander Woo (True Blood). En cuanto a quienes quieran leer los libros, seguramente encontrarán que muchas veces a la trilogía no se menciona como El recuerdo del pasado de la Tierra, sino directamente como El problema de los tres cuerpos. Aunque como ya se adelantaba, en este texto no hablaremos de la trilogía sino de Física.

Precedentes al problema de los tres cuerpos

El origen del problema de los tres cuerpos no es una novedad. Viene desde varios siglos atrás y se trata de un problema con un objetivo claro: determinar el movimiento de tres objetos en el espacio bajo la influencia conjunta de su atracción gravitatoria. Por muy sencillo que pueda parecer, a día de hoy no existe una solución analítica con la que obtener una expresión general. Es decir, no existe una fórmula que se pueda adaptar a estas condiciones. Lo que sí que se ha logrado es obtener simulaciones numéricas particularizadas a cada situación, las cuales permiten simular aproximaciones de aspectos tan dispares como la formación de sistemas planetarios, la evolución de estrellas o la dinámica de sistemas caóticos. Sin embargo, antes de abordar el problema como tal, me gustaría mencionar los precedentes que llevaron al planteamiento del problema y así ponerlo en contexto.

La Tierra en el centro

Los primeros planteamientos de los mecanismos celestes marcaron el camino que siglos más tarde llevaron a plantear el problema de los tres cuerpos. Recordemos que Aristóteles (s. IV a. C) propuso un modelo geocéntrico del universo donde la Tierra era el centro y el resto (Sol, planetas y estrellas) giraba alrededor de nuestro planeta. El máximo apogeo de esta corriente de pensamiento se tuvo con Claudio Ptolomeo (s. II d. C) y su obra Almagesto, donde describe minuciosamente el movimiento planetario.

El origen de la Trigonometría

Entre Aristóteles y Ptolomeo encontramos a Hiparco de Nicea (s. II a. C.). La historia lo recuerda, entre otras cosas, como el creador de la Trigonometría. De hecho, la aplica al cálculo de posiciones planetarias, obteniendo una gran precisión en los resultados. Al fin y al cabo, el geocentrismo no es más que una variante del heliocentrismo modificando el sistema de referencia. Con esto no quiero decir que el heliocentrismo no es válido. Por supuesto que lo es ya que en el universo, los cuerpos más masivos se ven orbitados por los de menor masa en función de la distancia que los separa. Y en el sistema solar, el más masivo -con diferencia- es el Sol. Además, el sistema heliocéntrico es mucho más sencillo y elegante que el geocéntrico.

La Edad Media y el heliocentrismo

El geocentrismo comenzó a tambalearse con la llegada de Copérnico y Galileo cuando publicaron sus obras De revolutionibus orbium coelestium en 1543 y Sidereus nuncius en 1610, respetivamente. Más tarde, Kepler primero y Newton después, con sus leyes pusieron números y afinaron las teorías heliocéntricas de sus predecesores. De hecho, Newton se basó en las Leyes de Kepler y este hizo lo propio tomando como base las ideas de Copérnico y Galileo. Una de las fechas más apoyadas por la comunidad científica y filosófica como el establecimiento del heliocentrismo es el 5 de julio de 1687, día en el que Newton publicó su Philosophiæ naturalis principia mathematica donde podemos encontrar su Ley de la Gravitación Universal, mostrando numéricamente cómo los planetas orbitan alrededor del Sol.

A partir de entonces, con un sistema solar modelado tanto a nivel cualitativo como a nivel cuantitativo, varios científicos estudiaron las interacciones entre varios cuerpos. Con dos objetos, los cálculos eran relativamente sencillos. Sin embargo, cuando entraban en juego tres o más cuerpos no se lograba llegar a una solución generalizada, tal y como ocurría con dos elementos. El problema de los tres cuerpos acababa de surgir.

Planteando el problema de los tres cuerpos

Ante la complejidad que planteaban estas situaciones con más de dos objetos en interacción, las Matemáticas y la Física navegaron juntas con el objetivo de plantear una solución generalizada. Tenemos que explorar a lo largo de los siglos XVIII y XIX para encontrar a tres de las personas que sentaron las bases de lo que hoy se conoce como el problema de los tres cuerpos:

• Leonhard Euler (1707-1783). En 1767 desarrolló sus ecuaciones para describir el movimiento de tres cuerpos de cualquier masa que se mueven en el mismo sentido a lo largo de una recta inmóvil.
• Joseph-Louis Lagrange (1736-1813). En 1772 desarrolló dos soluciones diferentes y periódicas, cada una de ellas para solucionar problemas con tres cuerpos. En una de ellas, los cuerpos se sitúan a lo largo de una recta, como en el caso de Euler, aunque planteada de forma más generalista. En la otra, los tres cuerpos se sitúan en los vértices de un triángulo equilátero en rotación.
• William Rowan Hamilton (1805-1869). En 1834 desarrolló las ecuaciones que llevan su nombre, que están descritas de un modo más general que las de Lagrange donde se describen los movimientos de sistemas mecánicos. Gracias a estas ecuaciones aplicadas a tres cuerpos, sentó las bases de las simulaciones numéricas que hoy intentan dar solución al problema.

Abordando el problema de los tres cuerpos

Ya nos podemos hacer una idea de que calcular los movimientos de tres cuerpos influidos por el campo gravitatorio de cada uno de ellos, no era tarea fácil. Uno de los inconvenientes es la fuerza de la gravedad porque, a pesar de que es la más evidente de las cuatro fuerzas fundamentales, es tan compleja que aún hoy no se tiene totalmente caracterizada. Por eso, la incertidumbre y el desconocimiento que hay a la hora de comprender la gravedad, hace que algunos movimientos resulten impredecibles, sobre todo cuando hay tres o más objetos interactuando.

Poco a poco se está viendo por qué resulta tan complicado encontrar una solución general a este problema. Tras los análisis que se hacen para estudiarlo, se obtienen unas ecuaciones tan complejas que en muchos casos son inabordables y, además, tan solo solucionan un caso extremadamente particular sin llegar a una solución general. Por eso, ante la falta de una expresión que lo modele, se utilizan simuladores numéricos para tener una aproximación y aunque estas simulaciones no sean tan precisas como lo sería una expresión general, abordando así el problema de los tres cuerpos ha permitido comprender la estabilidad orbital y la posibilidad de colisiones de objetos celestes, entre otras muchísimas cosas.

Beneficios de investigar el problema de los tres cuerpos

Gracias a la investigación que se ha hecho para comprender y resolver el problema de los tres cuerpos, varios campos se han visto beneficiados. Incluso a pesar de que el problema no se ha solucionado a día de hoy, las aproximaciones a las que se han llegado han permitido que varias disciplinas hayan avanzado en sus líneas científico-técnicas. Aquí se muestran algunas de ellas.

Formación de sistemas planetarios

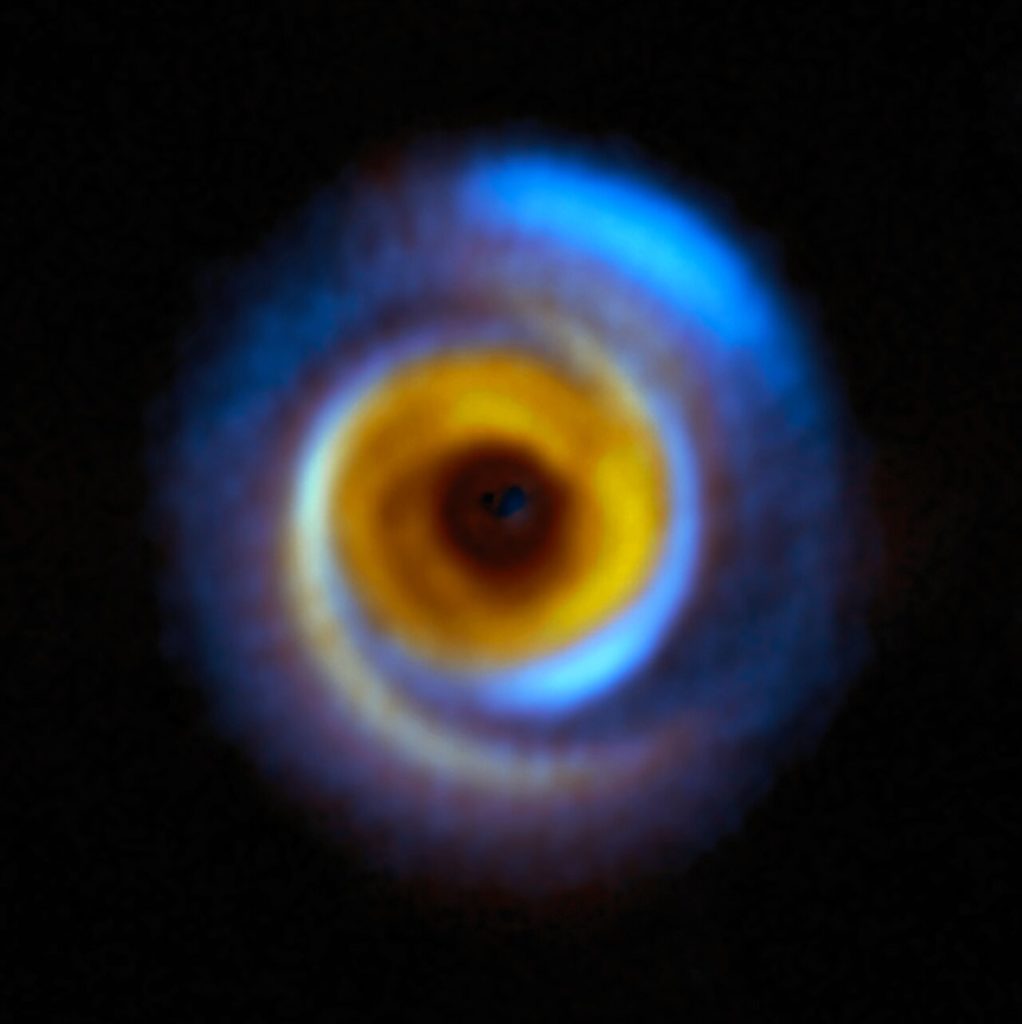
El problema de los tres cuerpos, si bien no ofrece una solución general, actúa como un potente método de análisis para comprender la formación de sistemas planetarios. A través de simulaciones computacionales se puede observar cómo la interacción gravitatoria de grupos de tres cuerpos puede dar lugar a la formación de discos protoplanetarios. Gracias a estos análisis se puede calcular la estabilidad de las órbitas y ver las posibilidades de que exista una colisión o averiguar qué orbitas tendrán los planetas una vez se hayan formado.

Ejemplos

• Sistemas peculiares. Existen simulaciones para interpretar la formación planetaria donde se utiliza el problema de los tres cuerpos. Por ejemplo, una simulación donde un disco protoplanetario de una estrella binaria donde el tercer cuerpo es un planeta en formación.
• Planetas gigantes. Utilizando el problema de los tres cuerpos, se puede modelar cómo será la evolución de un protoplaneta destinado a ser un exoplaneta gigante. Los resultados ofrecen que discos con una mayor masa inicial son más propensos a formar este tipo de planetas y en el caso de ser un sistema binario, las estrellas pequeñas dificultan la formación de este tipo de objetos.

Evolución de estrellas y galaxias

El estudio del problema de los tres cuerpos, permite obtener información relevante para comprender la evolución de estrellas y galaxias.

Con respecto a las estrellas, las simulaciones permiten analizar cómo es la interacción gravitatoria entre estrellas o cúmulos de estrellas. De este modo se pueden llegar a predecir ciertos movimientos o comportamientos, lo que ayuda a comprender su dinámica celeste y evolución. También permite analizar por separado sistemas binarios o ternarios y ver cómo van interactuando cada una de las partes.

En el análisis de las galaxias, el problema de los tres cuerpos ofrece simulaciones sobre cómo se forman estructuras que existen en estos grandes objetos como las barras, las espirales o los halos.

Ejemplos

• Formación de estrellas binarias. Se ha utilizado el problema de los tres cuerpos para simular la formación de estrellas binarias, encontrando cómo este tipo de sistemas puede formarse a partir de una nube de gas y polvo colapsando bajo su propia gravedad.
• Evolución de cúmulos globulares. La formación de cúmulos globulares y su evolución es un tema donde suele aplicarse el problema de los tres cuerpos. Gracias a las simulaciones se puede ver cómo interactúan unas estrellas con otras para mantenerse en una estructura esférica sin deformarse.

Dinámica de sistemas caóticos

Antes de nada, ¿qué es un sistema caótico? Se trata de un sistema en movimiento cuyo comportamiento es tan complejo que resulta impredecible bajo las leyes físicas conocidas. Por lo tanto, podemos predecir el comportamiento durante un rango de tiempo extremadamente corto; más allá, resulta impredecible.

Ahora bien, ¿cómo ayuda el estudio del problema de los tres cuerpos en los sistemas caóticos? La clave es que el problema de los tres cuerpos es un sistema caótico en sí mismo. Es decir, resulta complejo predecir el comportamiento de tres cuerpos más allá de un tiempo determinado. Por lo tanto, el estudiar este sistema caótico en concreto ofrece algunas herramientas para abordar otros de su misma naturaleza. Gracias a ello, ahora se pueden identificar algunos de los parámetros que controlan el sistema de estudio, identificar los distintos comportamientos que podría llegar a presentar o predecir un comportamiento determinado a corto plazo.

Ejemplos

• Clima terrestre. La climatología es un sistema caótico que depende de una gran cantidad de factores que deben ser medidos con una precisión extrema, como la temperatura, la presión, la humedad o la radiación solar. El problema de los tres cuerpos se ha utilizado para estudiar la dinámica del clima terrestre y hacer predicciones más afinadas.
• Poblaciones de animales. El estudio de la dinámica poblacional de animales son sistemas caóticos que están influenciados por factores como la disponibilidad de alimentos, la depredación y las enfermedades. Para estudiar la dinámica de estas poblaciones y poder dar una predicción de cómo podrían cambiar en un período de tiempo, se utilizan modelos obtenidos en el problema de los tres cuerpos.

Diseño de misiones espaciales

El diseño de de misiones espaciales, sobre todo las que tienen un cuerpo como objetivo, son un ejemplo del problema de los tres cuerpos: la Tierra, la sonda y el cuerpo de destino. Los modelos numéricos que se usan para simularlo han resultado fundamentales para el diseño de estas misiones. De esta forma, se puede simular la dinámica del movimiento de los tres cuerpos, algo fundamental para planificar trayectorias eficientes y seguras para las sondas. Además de calcular las trayectorias para evitar colisiones, también permite estimar el combustible necesario para la misión e identificar las ventanas de lanzamiento más favorables. De esto se deriva que también es importante a la hora de elegir el tipo de propulsor que resulte más eficiente para la misión.

Ejemplos

• Misión Rosetta (ESA). El cálculo de la trayectoria para llegar al cometa 67P/Churyumov-Gerasimenko, se realizó utilizando el problema de los tres cuerpos.
• Misión Dawn (NASA). La trayectoria de la sonda para orbitar los asteroides Vesta y Ceres se obtuvo aplicando el problema de los tres cuerpos.

Búsqueda de exoplanetas

El problema de los tres cuerpos nos ayuda a comprender la dinámica de los sistemas exoplanetarios, lo que es esencial para identificar las señales que indican la presencia de un planeta extrasolar y así poder marcar las limitaciones de los diferentes métodos de detección. Del mismo modo, permite desarrollar los métodos existentes para confirmar la presencia de exoplanetas de un modo eficaz siempre que se encuentre dentro de esos límites. Esto es de gran ayuda para caracterizar propiedades tales como la masa, el tamaño o la composición.

Las nuevas tecnologías, como la computación cuántica, podrán obtener series más precisas para abordar el problema de los tres cuerpos, lo que tendrá implicaciones en la detección de exoplanetas, lo que conduciría a encontrar cuerpos aún más similares a la Tierra.

Ejemplos

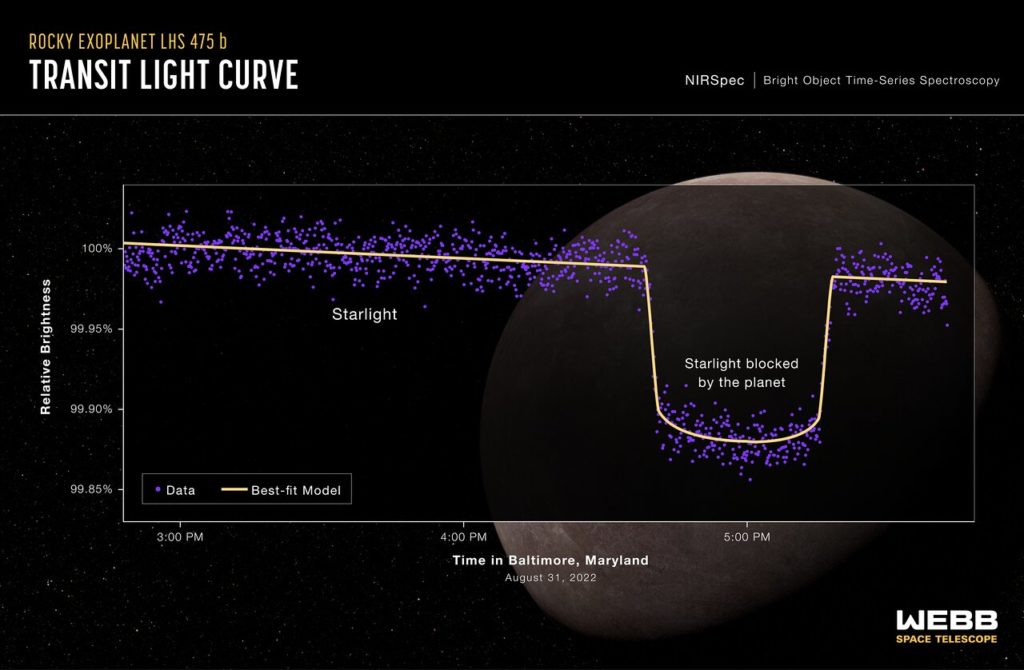
• Método del tránsito. La profundidad de la curva de luz del exoplaneta, es decir, la distancia entre la zona donde empieza la caída y el mínimo de la curva, se calcula utilizando el problema de los tres cuerpos.
• Método de las velocidades radiales. La velocidad radial de la estrella, efecto provocado por el hecho de tener un exoplaneta orbitando, se calcula mediante el problema de los tres cuerpos.

¿Por qué genera interés el problema de los tres cuerpos?

Ante la simpleza que pueda desprenderse a priori de un problema aparentemente sencillo como es el «problema de los tres cuerpos», es algo que trae de cabeza a científicos, matemáticos e incluso a filósofos como ya se ha podido deducir a lo largo de este texto.

Por un lado, el problema de los tres cuerpos ha sido y es un desafío matemático que ha intrigado incluso a las mentes más brillantes. Para intentar resolverlo se han desarrollado distintas técnicas que van desde las soluciones analíticas hasta las simulaciones numéricas. Sin embargo, como ya se ha comentado, no hay una respuesta definitiva a este problema.

Por último, y ya para terminar, a pesar de la complejidad que representa el problema de los tres cuerpos, es un marco que se basa en unos principios físicos extremadamente simples. No cabe duda que es un ejemplo de cómo las leyes de la Física a partir de un supuesto sencillo pueden dar lugar a comportamientos complejos, inesperados y caóticos.